Note

Go to the end to download the full example code.

Fourier Differentiation

An example of usage of our Fourier Differentiation Function

Import the library

We first import our neuralop library and required dependencies.

import torch
import numpy as np
import matplotlib.pyplot as plt
from neuralop.losses.differentiation import FourierDiff

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Creating an example of periodic 1D curve

Here we consider sin(x) and cos(x), which are periodic on the interval [0, 2π]

L = 2 * torch.pi
x = torch.linspace(0, L, 101)[:-1]
f = torch.stack([torch.sin(x), torch.cos(x)], dim=0)
x_np = x.cpu().numpy()

Differentiate the signal

We use the FourierDiff class to differentiate the signal

fd1d = FourierDiff(dim=1, L=L, use_fc=False)
derivatives = fd1d.compute_multiple_derivatives(f, [1, 2, 3])
dfdx, df2dx2, df3dx3 = derivatives

Plot the results for sin(x)

plt.figure()
plt.plot(x_np, dfdx[0].squeeze().cpu().numpy(), label='Fourier dfdx')
plt.plot(x_np, np.cos(x_np), '--', label='dfdx')
plt.plot(x_np, df2dx2[0].squeeze().cpu().numpy(), label='Fourier df2dx2')
plt.plot(x_np, -np.sin(x_np), '--', label='df2dx2')
plt.plot(x_np, df3dx3[0].squeeze().cpu().numpy(), label='Fourier df3dx3')
plt.plot(x_np, -np.cos(x_np), '--', label='df3dx3')
plt.xlabel('x')
plt.legend()
plt.show()
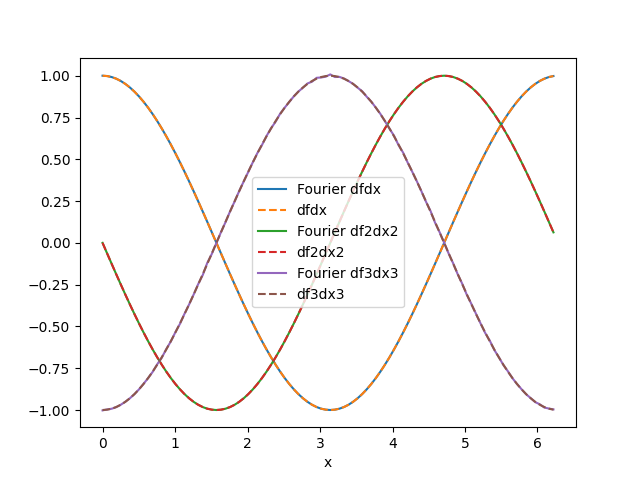
plot fourier diff

Plot the results for cos(x)

plt.figure()
plt.plot(x_np, dfdx[1].squeeze().cpu().numpy(), label='Fourier dfdx')
plt.plot(x_np, -np.sin(x_np), '--', label='dfdx')
plt.plot(x_np, df2dx2[1].squeeze().cpu().numpy(), label='Fourier df2dx2')
plt.plot(x_np, -np.cos(x_np), '--', label='df2dx2')
plt.plot(x_np, df3dx3[1].squeeze().cpu().numpy(), label='Fourier df3dx3')
plt.plot(x_np, np.sin(x_np), '--', label='df3dx3')
plt.xlabel('x')
plt.legend()
plt.show()
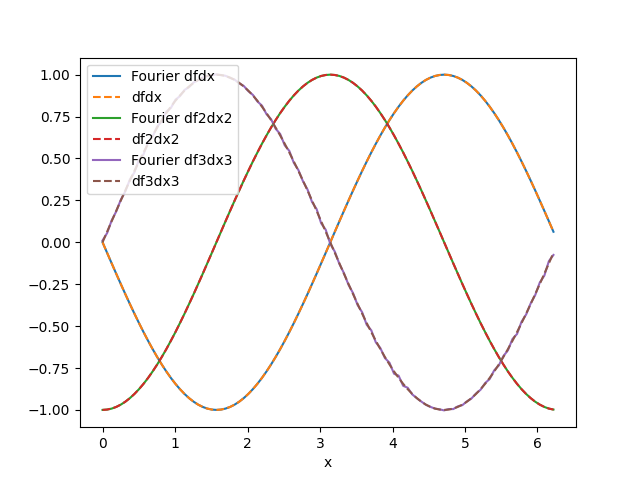
plot fourier diff

Creating an example of non-periodic 1D curve

Here we consider sin(3x)-cos(x) and exp(-0.8x)+sin(x)

L = 2 * torch.pi
x = torch.linspace(0, L, 101)[:-1]
f = torch.stack([torch.sin(3*x) - torch.cos(x), torch.exp(-0.8*x) + torch.sin(x)], dim=0)
x_np = x.cpu().numpy()

Differentiate the signal

We use the FourierDiff class with Fourier continuation to differentiate the signal

fd1d = FourierDiff(dim=1, L=L, use_fc='Legendre', fc_degree=4, fc_n_additional_pts=50)
derivatives = fd1d.compute_multiple_derivatives(f, [1, 2])
dfdx, df2dx2 = derivatives

Plot the results for sin(3x)-cos(x)

plt.figure()
plt.plot(x_np, dfdx[0].squeeze().cpu().numpy(), label='Fourier dfdx')
plt.plot(x_np, 3*torch.cos(3*x) + torch.sin(x), '--', label='dfdx')
plt.plot(x_np, df2dx2[0].squeeze().cpu().numpy(), label='Fourier df2dx2')
plt.plot(x_np, -9*torch.sin(3*x) + torch.cos(x), '--', label='df2dx2')
plt.xlabel('x')
plt.legend()
plt.show()
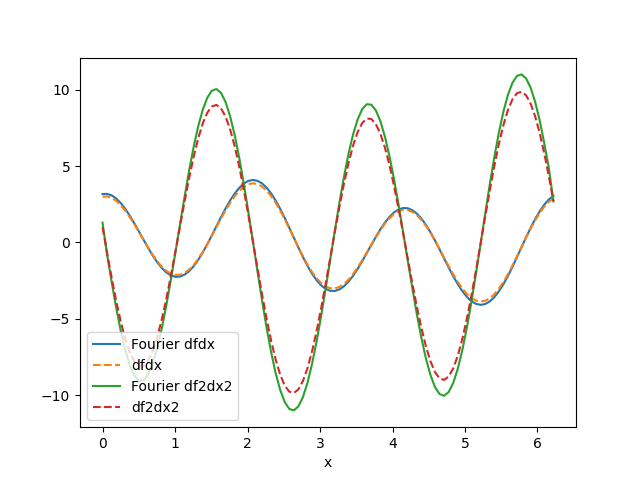
plot fourier diff

Plot the results for exp(-0.8x)+sin(x)

plt.figure()
plt.plot(x_np, dfdx[1].squeeze().cpu().numpy(), label='Fourier dfdx')
plt.plot(x_np, -0.8*torch.exp(-0.8*x)+torch.cos(x), '--', label='dfdx')
plt.plot(x_np, df2dx2[1].squeeze().cpu().numpy(), label='Fourier df2dx2')
plt.plot(x_np, 0.64*torch.exp(-0.8*x)-torch.sin(x), '--', label='df2dx2')
plt.xlabel('x')
plt.legend()
plt.show()
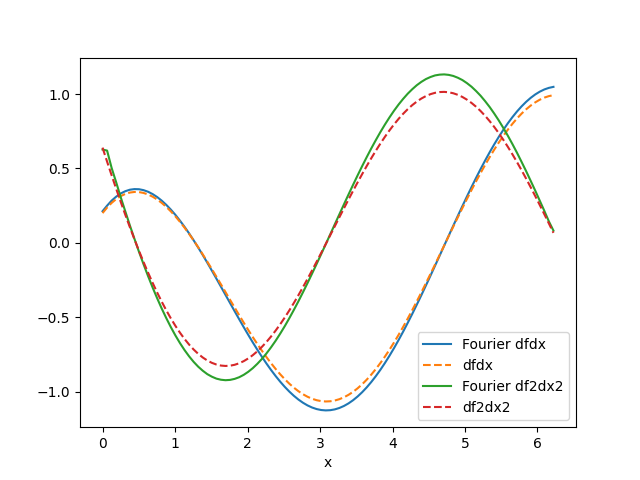
plot fourier diff

2D Fourier Differentiation Examples

Here we demonstrate the FourierDiff class for 2D functions

Creating an example of periodic 2D function

Here we consider f(x,y) = sin(x) * cos(y), which is periodic on the interval [0, 2π] × [0, 2π]

L_x, L_y = 2 * torch.pi, 2 * torch.pi
nx, ny = 180, 186
x = torch.linspace(0, L_x, nx, dtype=torch.float64)
y = torch.linspace(0, L_y, ny, dtype=torch.float64)
X, Y = torch.meshgrid(x, y, indexing='ij')

# Test function: f(x,y) = sin(x) * cos(y)
f_2d = torch.sin(X) * torch.cos(Y)

Differentiate the 2D signal

We use the FourierDiff class to compute derivatives

fd2d = FourierDiff(dim=2, L=(L_x, L_y))

# Compute derivatives
df_dx = fd2d.dx(f_2d)
df_dy = fd2d.dy(f_2d)
laplacian = fd2d.laplacian(f_2d)

# Expected analytical results for f(x,y) = sin(x) * cos(y)
df_dx_expected = torch.cos(X) * torch.cos(Y)
df_dy_expected = -torch.sin(X) * torch.sin(Y)
laplacian_expected = -2 * torch.sin(X) * torch.cos(Y)

Plot the 2D results

fig, axes = plt.subplots(2, 3, figsize=(15, 10))
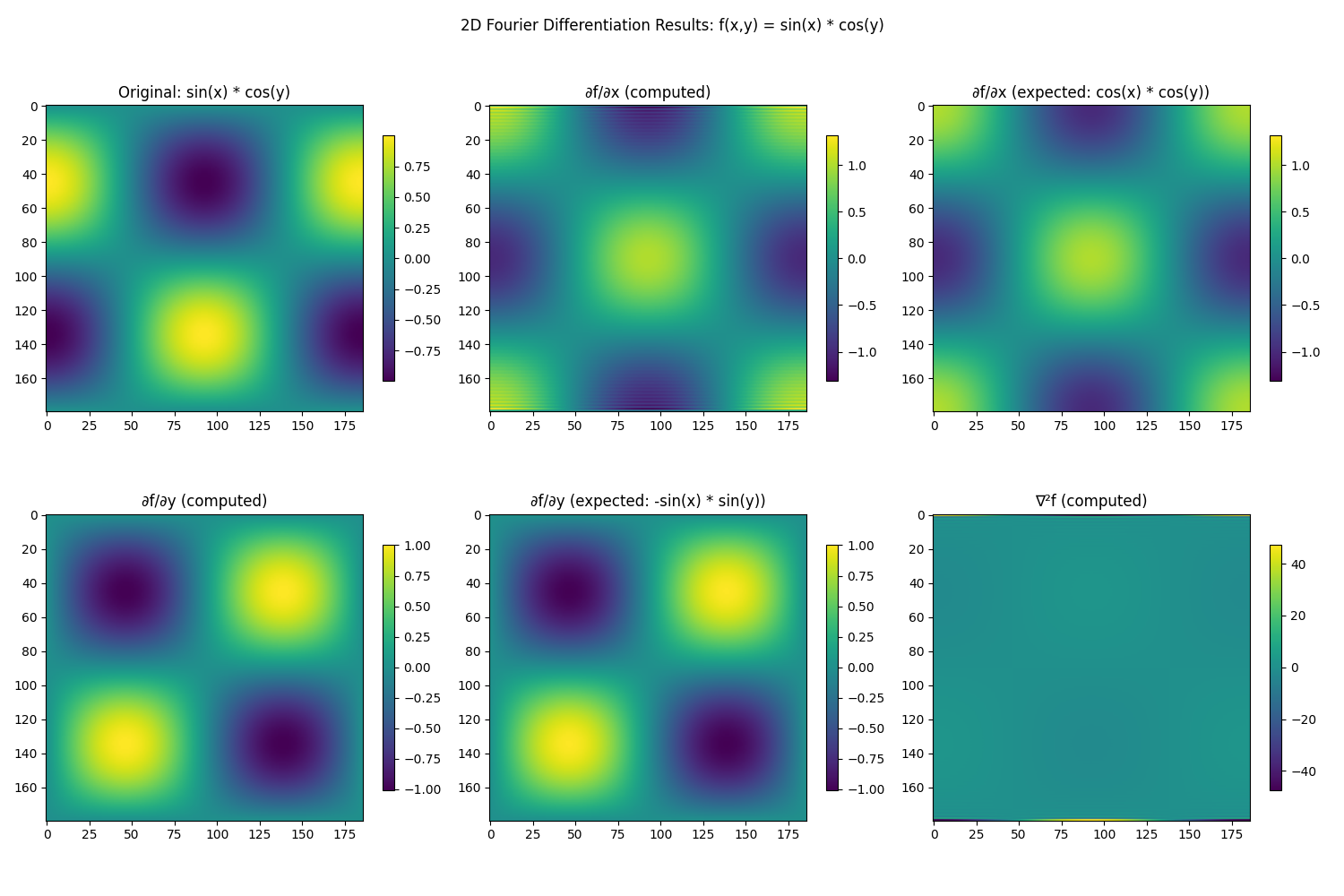
fig.suptitle('2D Fourier Differentiation Results: f(x,y) = sin(x) * cos(y)')

# Compute consistent colorbar limits for each derivative pair
df_dx_min = min(df_dx.min().item(), df_dx_expected.min().item())
df_dx_max = max(df_dx.max().item(), df_dx_expected.max().item())
df_dy_min = min(df_dy.min().item(), df_dy_expected.min().item())
df_dy_max = max(df_dy.max().item(), df_dy_expected.max().item())

# Original function
im0 = axes[0, 0].imshow(f_2d.cpu().numpy())
axes[0, 0].set_title('Original: sin(x) * cos(y)')
plt.colorbar(im0, ax=axes[0, 0], shrink=0.57)

# ∂f/∂x computed
im1 = axes[0, 1].imshow(df_dx.cpu().numpy(), vmin=df_dx_min, vmax=df_dx_max)
axes[0, 1].set_title('∂f/∂x (computed)')
plt.colorbar(im1, ax=axes[0, 1], shrink=0.57)

# ∂f/∂x expected
im2 = axes[0, 2].imshow(df_dx_expected.cpu().numpy(), vmin=df_dx_min, vmax=df_dx_max)
axes[0, 2].set_title('∂f/∂x (expected: cos(x) * cos(y))')
plt.colorbar(im2, ax=axes[0, 2], shrink=0.57)

# ∂f/∂y computed
im3 = axes[1, 0].imshow(df_dy.cpu().numpy(), vmin=df_dy_min, vmax=df_dy_max)
axes[1, 0].set_title('∂f/∂y (computed)')
plt.colorbar(im3, ax=axes[1, 0], shrink=0.57)

# ∂f/∂y expected
im4 = axes[1, 1].imshow(df_dy_expected.cpu().numpy(), vmin=df_dy_min, vmax=df_dy_max)
axes[1, 1].set_title('∂f/∂y (expected: -sin(x) * sin(y))')
plt.colorbar(im4, ax=axes[1, 1], shrink=0.57)

# Laplacian
im5 = axes[1, 2].imshow(laplacian.cpu().numpy())
axes[1, 2].set_title('∇²f (computed)')
plt.colorbar(im5, ax=axes[1, 2], shrink=0.57)

plt.tight_layout()
plt.show()
2D Fourier Differentiation Results: f(x,y) = sin(x) * cos(y), Original: sin(x) * cos(y), ∂f/∂x (computed), ∂f/∂x (expected: cos(x) * cos(y)), ∂f/∂y (computed), ∂f/∂y (expected: -sin(x) * sin(y)), ∇²f (computed)

3D Fourier Differentiation Examples

Here we demonstrate the FourierDiff class for 3D functions

Creating an example of periodic 3D function

Here we consider f(x,y,z) = sin(x) * cos(y) * sin(z), which is periodic on [0, 2π]³

L_x, L_y, L_z = 2 * torch.pi, 2 * torch.pi, 2 * torch.pi
nx, ny, nz = 176, 180, 192
x = torch.linspace(0, L_x, nx, dtype=torch.float64)
y = torch.linspace(0, L_y, ny, dtype=torch.float64)
z = torch.linspace(0, L_z, nz, dtype=torch.float64)
X, Y, Z = torch.meshgrid(x, y, z, indexing='ij')

# Test function: f(x,y,z) = sin(x) * cos(y) * sin(z)
f_3d = torch.sin(X) * torch.cos(Y) * torch.sin(Z)

# Alternative: create tensor directly like in the test
f_3d_alt = torch.randn(nx, ny, nz, dtype=torch.float64)

Differentiate the 3D signal

We use the FourierDiff class to compute derivatives

fd3d = FourierDiff(dim=3, L=(L_x, L_y, L_z))

# Compute derivatives
df_dx_3d = fd3d.dx(f_3d)
df_dy_3d = fd3d.dy(f_3d)
df_dz_3d = fd3d.dz(f_3d)
laplacian_3d = fd3d.laplacian(f_3d)

# Expected analytical results for f(x,y,z) = sin(x) * cos(y) * sin(z)
df_dx_expected_3d = torch.cos(X) * torch.cos(Y) * torch.sin(Z)
df_dy_expected_3d = -torch.sin(X) * torch.sin(Y) * torch.sin(Z)
df_dz_expected_3d = torch.sin(X) * torch.cos(Y) * torch.cos(Z)
laplacian_expected_3d = -3 * torch.sin(X) * torch.cos(Y) * torch.sin(Z)

Plot a slice of the 3D results (z=0 plane)

z_slice_idx = nz // 2
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
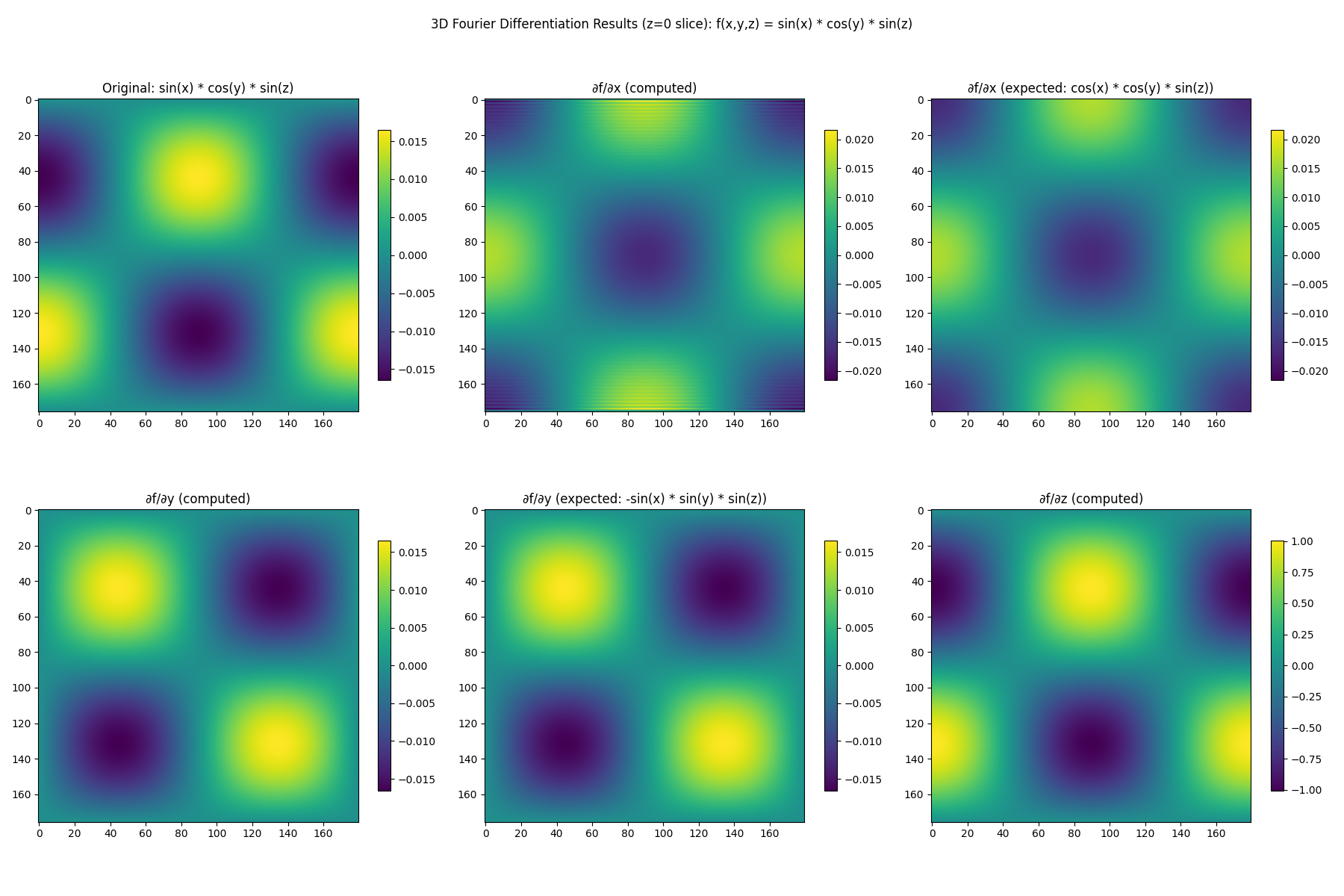
fig.suptitle('3D Fourier Differentiation Results (z=0 slice): f(x,y,z) = sin(x) * cos(y) * sin(z)')

# Compute consistent colorbar limits for each derivative pair at the z-slice
df_dx_3d_slice = df_dx_3d[:, :, z_slice_idx]
df_dx_expected_3d_slice = df_dx_expected_3d[:, :, z_slice_idx]
df_dy_3d_slice = df_dy_3d[:, :, z_slice_idx]
df_dy_expected_3d_slice = df_dy_expected_3d[:, :, z_slice_idx]

df_dx_3d_min = min(df_dx_3d_slice.min().item(), df_dx_expected_3d_slice.min().item())
df_dx_3d_max = max(df_dx_3d_slice.max().item(), df_dx_expected_3d_slice.max().item())
df_dy_3d_min = min(df_dy_3d_slice.min().item(), df_dy_expected_3d_slice.min().item())
df_dy_3d_max = max(df_dy_3d_slice.max().item(), df_dy_expected_3d_slice.max().item())

# Original function slice
im0 = axes[0, 0].imshow(f_3d[:, :, z_slice_idx].cpu().numpy())
axes[0, 0].set_title('Original: sin(x) * cos(y) * sin(z)')
plt.colorbar(im0, ax=axes[0, 0], shrink=0.57)

# ∂f/∂x slice
im1 = axes[0, 1].imshow(df_dx_3d_slice.cpu().numpy(), vmin=df_dx_3d_min, vmax=df_dx_3d_max)
axes[0, 1].set_title('∂f/∂x (computed)')
plt.colorbar(im1, ax=axes[0, 1], shrink=0.57)

# ∂f/∂x expected slice
im2 = axes[0, 2].imshow(df_dx_expected_3d_slice.cpu().numpy(), vmin=df_dx_3d_min, vmax=df_dx_3d_max)
axes[0, 2].set_title('∂f/∂x (expected: cos(x) * cos(y) * sin(z))')
plt.colorbar(im2, ax=axes[0, 2], shrink=0.57)

# ∂f/∂y slice
im3 = axes[1, 0].imshow(df_dy_3d_slice.cpu().numpy(), vmin=df_dy_3d_min, vmax=df_dy_3d_max)
axes[1, 0].set_title('∂f/∂y (computed)')
plt.colorbar(im3, ax=axes[1, 0], shrink=0.57)

# ∂f/∂y expected slice
im4 = axes[1, 1].imshow(df_dy_expected_3d_slice.cpu().numpy(), vmin=df_dy_3d_min, vmax=df_dy_3d_max)
axes[1, 1].set_title('∂f/∂y (expected: -sin(x) * sin(y) * sin(z))')
plt.colorbar(im4, ax=axes[1, 1], shrink=0.57)

# ∂f/∂z slice
im5 = axes[1, 2].imshow(df_dz_3d[:, :, z_slice_idx].cpu().numpy())
axes[1, 2].set_title('∂f/∂z (computed)')
plt.colorbar(im5, ax=axes[1, 2], shrink=0.57)

plt.tight_layout()
plt.show()
3D Fourier Differentiation Results (z=0 slice): f(x,y,z) = sin(x) * cos(y) * sin(z), Original: sin(x) * cos(y) * sin(z), ∂f/∂x (computed), ∂f/∂x (expected: cos(x) * cos(y) * sin(z)), ∂f/∂y (computed), ∂f/∂y (expected: -sin(x) * sin(y) * sin(z)), ∂f/∂z (computed)

Total running time of the script: (0 minutes 3.922 seconds)

Gallery generated by Sphinx-Gallery