Theory Guide
This section contains a comprehensive primer on the theoretical foundations of operator learning, an introduction to the Fourier Neural Operator, an exploration of the key advantages of neural operators, and a showcase of diverse applications across scientific and engineering domains. These guides provide the mathematical background and practical insights needed to understand neural operators for solving partial differential equations.
A comprehensive introduction to operator learning and neural operators.
Learn the mathematical foundations, kernel formulations, and how neural operators generalize across different discretizations to solve PDEs efficiently.
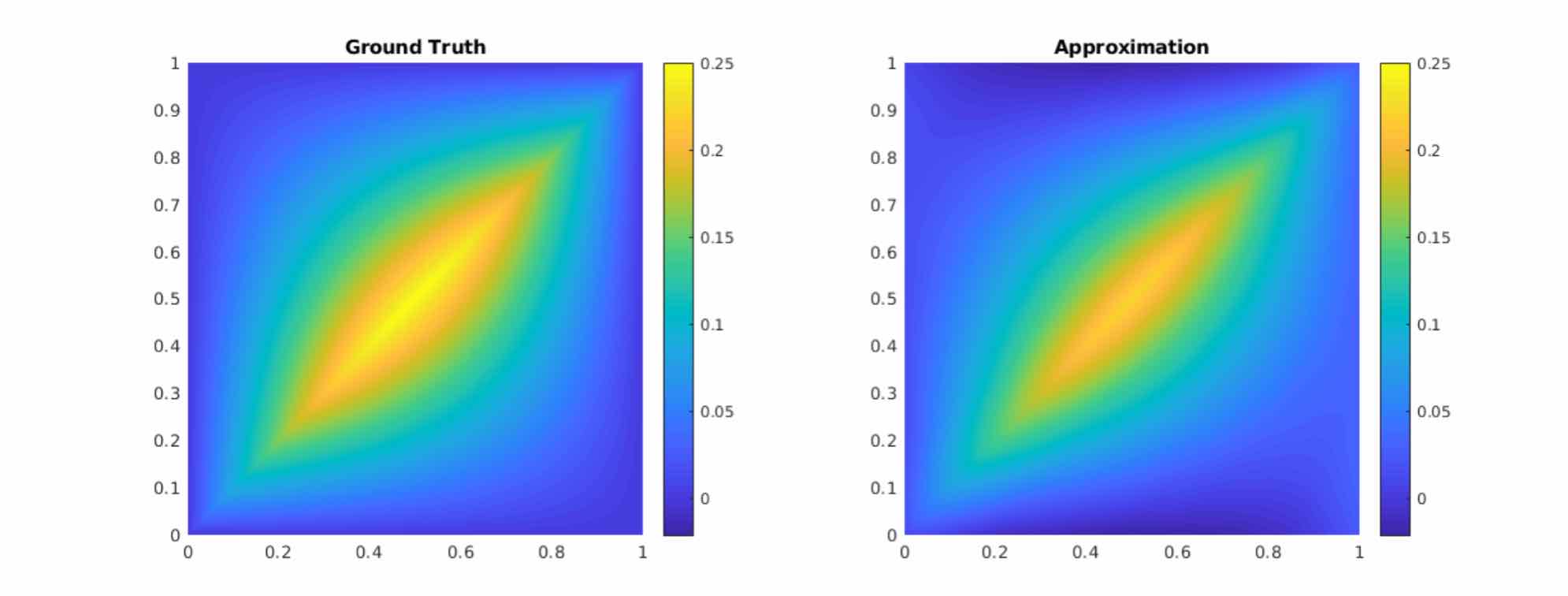
A practitioner’s guide to the Fourier Neural Operator.
Discover how FNOs achieve state-of-the-art performance on challenging PDEs like Navier-Stokes equations with up to 1000x speedup over traditional solvers.
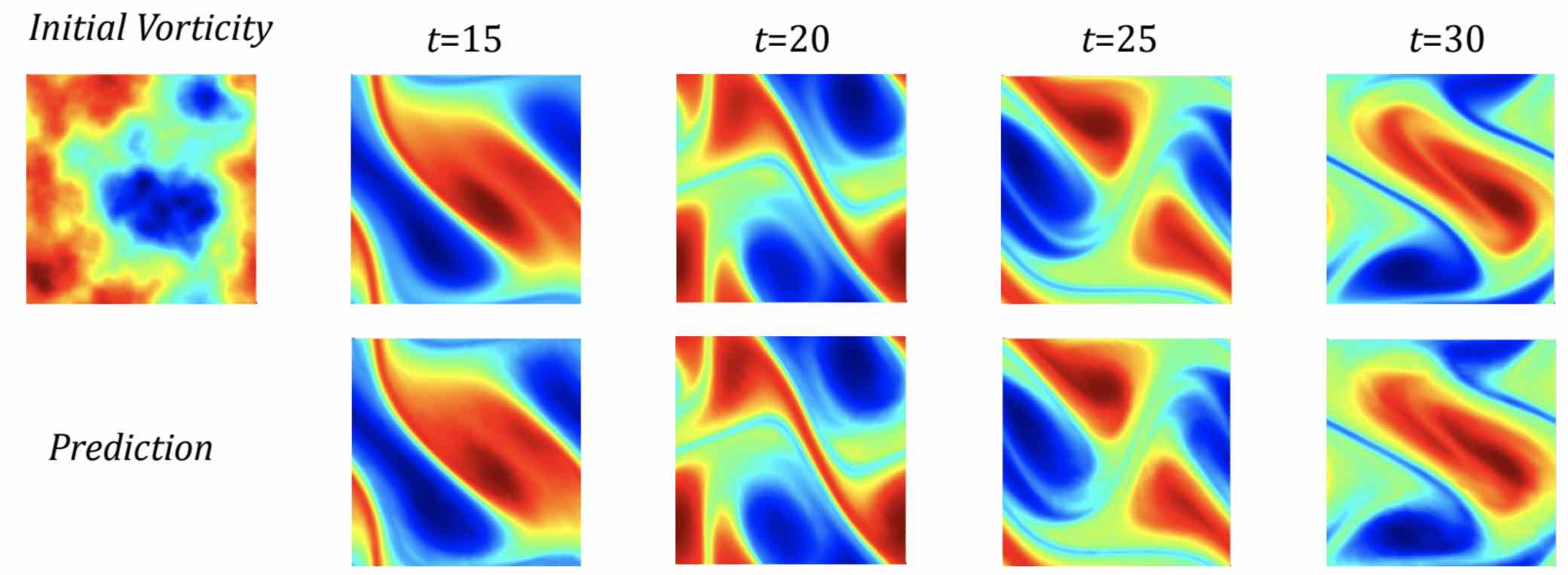
Explore the key advantages of neural operators over traditional methods.
Learn about resolution invariance, universal approximation, flexible inference, and data efficiency that make neural operators uniquely powerful for scientific computing.
Discover diverse examples of neural operator applications across scientific domains.
Explore real-world applications in fluid dynamics, climate modeling, materials science, biomedical engineering, and more, showcasing the transformative impact of neural operators.