DISCO Convolutions

This tutorial demonstrates Discrete-Continuous (DISCO) convolutions, which are the building blocks of localized neural operator frameworks. DISCO convolutions are crucial for:

Learning localized patterns in data
Handling both equidistant and unstructured grids
Enabling efficient computation on irregular domains
Bridging discrete and continuous representations

The tutorial covers various DISCO convolution types and their applications in neural operator architectures.

Preparation

import os
import torch
import torch.nn as nn
import numpy as np
import math
from functools import partial

from matplotlib import image

from torch_harmonics.quadrature import (
    legendre_gauss_weights,
    lobatto_weights,
    clenshaw_curtiss_weights,
)

import matplotlib.pyplot as plt

cmap = "inferno"
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

from neuralop.layers.discrete_continuous_convolution import (
    DiscreteContinuousConv2d,
    DiscreteContinuousConvTranspose2d,
    EquidistantDiscreteContinuousConv2d,
    EquidistantDiscreteContinuousConvTranspose2d,
)

Let’s start by loading an example image

os.system(
    "curl https://upload.wikimedia.org/wikipedia/commons/thumb/d/d3/Albert_Einstein_Head.jpg/360px-Albert_Einstein_Head.jpg -o ./einstein.jpg"
)

nx = 90
ny = 120

img = image.imread("./einstein.jpg")
data = nn.functional.interpolate(
    torch.from_numpy(img).unsqueeze(0).unsqueeze(0), size=(ny, nx)
).squeeze()
plt.imshow(data, cmap=cmap)
plt.show()

/home/runner/work/neuraloperator/neuraloperator/examples/layers/plot_DISCO_convolutions.py:70: UserWarning: The given NumPy array is not writable, and PyTorch does not support non-writable tensors. This means writing to this tensor will result in undefined behavior. You may want to copy the array to protect its data or make it writable before converting it to a tensor. This type of warning will be suppressed for the rest of this program. (Triggered internally at /pytorch/torch/csrc/utils/tensor_numpy.cpp:206.)
  torch.from_numpy(img).unsqueeze(0).unsqueeze(0), size=(ny, nx)

Let’s create a grid on which the data lives

x_in = torch.linspace(0, 2, nx)
y_in = torch.linspace(0, 3, ny)

x_in, y_in = torch.meshgrid(x_in, y_in, indexing="ij")
grid_in = torch.stack([x_in.reshape(-1), y_in.reshape(-1)])

# compute the correct quadrature weights
# IMPORTANT: this needs to be done right in order for the DISCO convolution to be normalized proeperly
w_x = 2 * torch.ones_like(x_in) / nx
w_y = 3 * torch.ones_like(y_in) / ny
q_in = (w_x * w_y).reshape(-1)

Visualize the grid

plt.figure(
    figsize=(4, 6),
)
plt.scatter(grid_in[0], grid_in[1], s=0.2)
plt.xlim(0, 2)
plt.ylim(0, 3)
plt.show()

Format data into the same format and plot it on the grid

data = data.permute(1, 0).flip(1).reshape(-1)

plt.figure(figsize=(4,6))
plt.tripcolor(grid_in[0], grid_in[1], data, cmap=cmap)
# plt.colorbar()
plt.xlim(0, 2)
plt.ylim(0, 3)
plt.show()

For the convolution output we require an output mesh

nxo = 90
nyo = 120

x_out = torch.linspace(0, 2, nxo)
y_out = torch.linspace(0, 3, nyo)

x_out, y_out = torch.meshgrid(x_out, y_out, indexing="ij")
grid_out = torch.stack([x_out.reshape(-1), y_out.reshape(-1)])

# compute the correct quadrature weights
w_x = 2 * torch.ones_like(x_out) / nxo
w_y = 3 * torch.ones_like(y_out) / nyo
q_out = (w_x * w_y).reshape(-1)

Initialize the convolution and set the weights to something resembling an edge filter/finit differences

conv = DiscreteContinuousConv2d(
    1,
    1,
    grid_in=grid_in,
    grid_out=grid_out,
    quadrature_weights=q_in,
    kernel_shape=[2, 4],
    radius_cutoff=5 / nyo,
    periodic=False,
).float()

# initialize a kernel resembling an edge filter
w = torch.zeros_like(conv.weight)
w[0, 0, 1] = 1.0
w[0, 0, 3] = -1.0
conv.weight = nn.Parameter(w)
psi = conv.get_local_filter_matrix()

Apply the DISCO convolution to the data and plot it in order to compute the convolved image, we need to first bring it into the right shape with batch_size x n_channels x n_grid_points

out = conv(data.reshape(1, 1, -1))

print(out.shape)

plt.figure(figsize=(4,6))
plt.imshow(torch.flip(out.squeeze().detach().reshape(nxo, nyo).transpose(0,1), dims=(-2, )), cmap=cmap)
plt.colorbar()
plt.show()

out1 = torch.flip(out.squeeze().detach().reshape(nxo, nyo).transpose(0, 1), dims=(-2,))

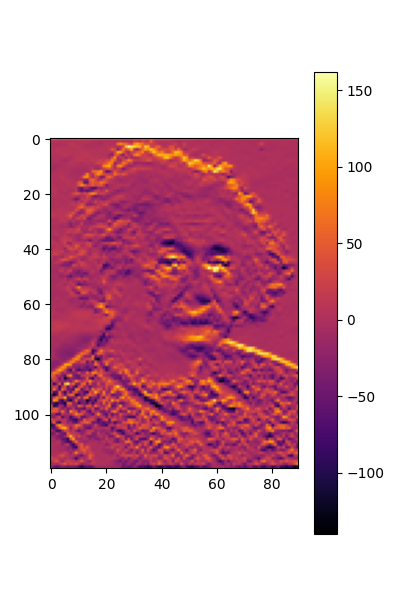
torch.Size([1, 1, 10800])

Do the same but on an equidistant grid

conv_equi = EquidistantDiscreteContinuousConv2d(
    1,
    1,
    (nx, ny),
    (nxo, nyo),
    kernel_shape=[2, 4],
    radius_cutoff=5 / nyo,
    domain_length=[2, 3],
)

# initialize a kernel resembling an edge filter
w = torch.zeros_like(conv.weight)
w[0, 0, 1] = 1.0
w[0, 0, 3] = -1.0
conv_equi.weight = nn.Parameter(w)

data = nn.functional.interpolate(
    torch.from_numpy(img).unsqueeze(0).unsqueeze(0), size=(ny, nx)
).float()

out_equi = conv_equi(data)

print(out_equi.shape)

plt.figure(figsize=(4,6))
plt.imshow(out_equi.squeeze().detach(), cmap=cmap)
plt.colorbar()
plt.show()

out2 = out_equi.squeeze().detach()

print(out2.shape)

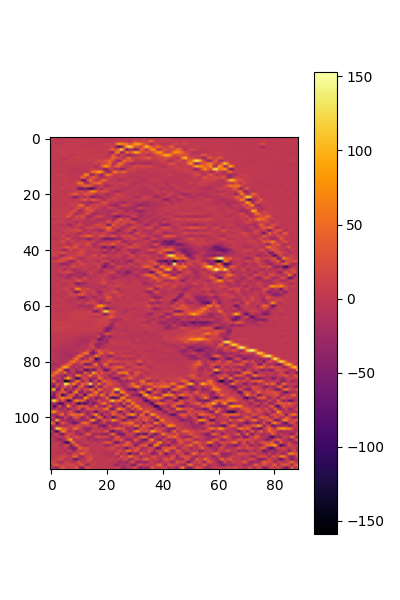
torch.Size([1, 1, 119, 89])
torch.Size([119, 89])

Visualize the local filter matrix

plt.figure(figsize=(4,6))
plt.imshow(conv_equi.get_local_filter_matrix()[0].detach(), cmap=cmap)
plt.colorbar()

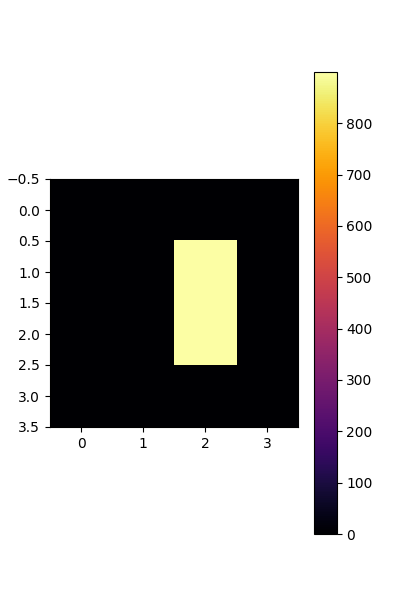
<matplotlib.colorbar.Colorbar object at 0x7f6064948410>

Test the transpose convolution

convt = DiscreteContinuousConvTranspose2d(
    1,
    1,
    grid_in=grid_out,
    grid_out=grid_in,
    quadrature_weights=q_out,
    kernel_shape=[2, 4],
    radius_cutoff=3 / nyo,
    periodic=False,
).float()

# initialize a flat
w = torch.zeros_like(conv.weight)
w[0, 0, 0] = 1.0
w[0, 0, 1] = 1.0
w[0, 0, 2] = 1.0
w[0, 0, 3] = 1.0
convt.weight = nn.Parameter(w)

data = (
    nn.functional.interpolate(
        torch.from_numpy(img).unsqueeze(0).unsqueeze(0), size=(ny, nx)
    )
    .squeeze().float()
    .permute(1, 0).flip(1).reshape(-1)
)
out = convt(data.reshape(1, 1, -1))

print(out.shape)

plt.figure(figsize=(4,6))
plt.imshow(torch.flip(out.squeeze().detach().reshape(nx, ny).transpose(0,1), dims=(-2, )), cmap=cmap)
plt.colorbar()
plt.show()

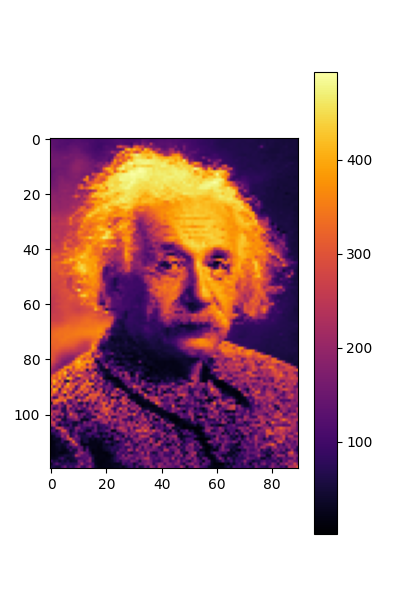
torch.Size([1, 1, 10800])

Test the equidistant transpose convolution

convt_equi = EquidistantDiscreteContinuousConvTranspose2d(
    1,
    1,
    (nxo, nyo),
    (nx, ny),
    kernel_shape=[2, 4],
    radius_cutoff=3 / nyo,
    domain_length=[2, 3],
)

# initialize a flat
w = torch.zeros_like(convt_equi.weight)
w[0, 0, 0] = 1.0
w[0, 0, 1] = 1.0
w[0, 0, 2] = 1.0
w[0, 0, 3] = 1.0
convt_equi.weight = nn.Parameter(w)

data = nn.functional.interpolate(
    torch.from_numpy(img).unsqueeze(0).unsqueeze(0), size=(nyo, nxo)
).float()
out_equi = convt_equi(data)

print(out_equi.shape)

plt.figure(figsize=(4,6))
plt.imshow(out_equi.squeeze().detach(), cmap=cmap)
plt.colorbar()
plt.show()

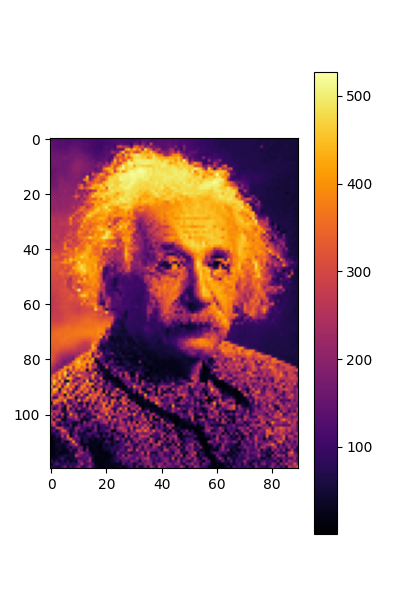
torch.Size([1, 1, 120, 90])

Total running time of the script: (0 minutes 29.277 seconds)

Gallery generated by Sphinx-Gallery