Note

Go to the end to download the full example code.

Fourier Continuation

This tutorial demonstrates Fourier continuation methods for extending non-periodic functions to periodic ones, enabling efficient spectral analysis and neural operator applications. Fourier continuation is crucial for:

  • Converting non-periodic data to periodic form

  • Enabling spectral methods on arbitrary domains

  • Improving convergence of Fourier-based neural operators

  • Handling boundary conditions in spectral computations

The tutorial covers both FC-Legendre and FC-Gram methods for 1D, 2D, and 3D data.

Import the library

We first import our neuralop library and required dependencies.

import torch
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from neuralop.layers.fourier_continuation import FCLegendre, FCGram


device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Creating an example of 1D non-periodic function

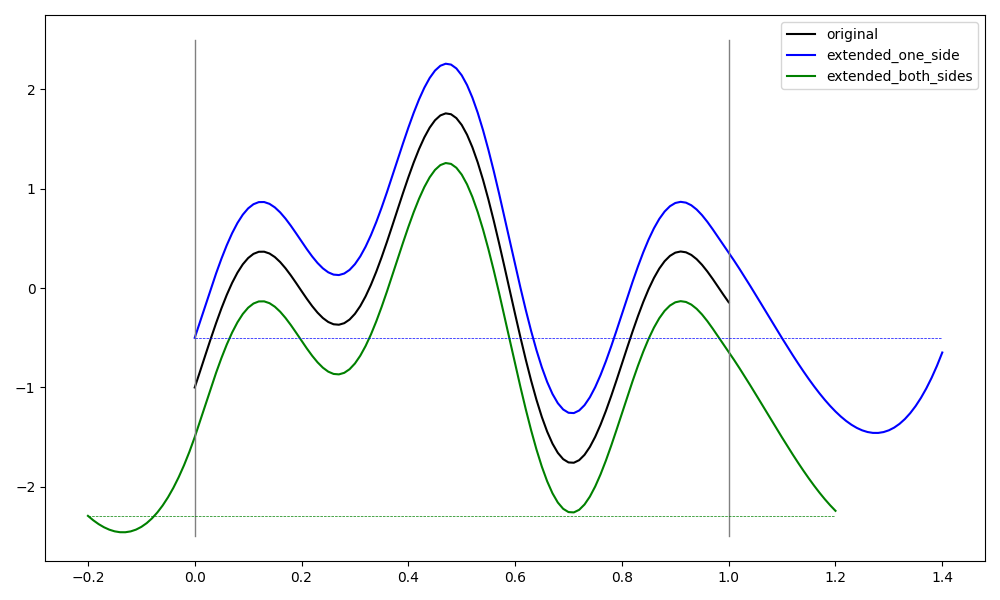
We consider f(x) = sin(16x) - cos(8x) on the interval [0,1]. This function is not periodic on [0,1], making it a good test case for Fourier continuation methods.

length_signal = 101  # Length of the original 1D signal
add_pts = 50  # Number of additional points for continuation
batch_size = 3  # Batch size for processing multiple signals

# Create the input signal
x = torch.linspace(0, 1, length_signal).repeat(batch_size, 1)
f = torch.sin(16 * x) - torch.cos(8 * x)

Extending the signal

We use the FC-Legendre and FC-Gram Fourier continuation layers to extend the signal.

# FC-Legendre: Uses Legendre polynomial basis for continuation
Extension_Legendre = FCLegendre(d=2, n_additional_pts=add_pts)
f_extend_Legendre = Extension_Legendre(f, dim=1)

# FC-Gram: Uses Gram polynomial basis for continuation
Extension_Gram = FCGram(d=4, n_additional_pts=add_pts)
f_extend_Gram = Extension_Gram(f, dim=1)

Visualizing the 1D Fourier continuation results

We plot the original function and both continuation methods to compare their effectiveness in creating smooth periodic extensions.

# Define the extended coordinates
x_extended = torch.linspace(-0.25, 1.25, 151)

# Adjust the extended functions for visualization purposes
f_extend_Legendre_adjusted = f_extend_Legendre - 0.6
f_extend_Gram_adjusted = f_extend_Gram + 0.6

plt.figure(figsize=(13, 6))
plt.plot(x[0], f[0], "k", label="Original Function", lw=2.2)
plt.plot(x_extended, f_extend_Gram_adjusted[0], "b", label="FC-Gram Extension", lw=2.2)
plt.plot(x_extended, f_extend_Legendre_adjusted[0], "g", label="FC-Legendre Extension", lw=2.2)
plt.plot([0, 0], [-2.9, 1.9], "-", color="gray", lw=1.5)
plt.plot([1, 1], [-2.9, 1.1], "-", color="gray", lw=1.5)
plt.plot([-0.25, 1.25], [f_extend_Legendre_adjusted[0, 0], f_extend_Legendre_adjusted[0, 0]], "--", color="g", lw=1.6)
plt.plot([-0.25, 1.25], [f_extend_Gram_adjusted[0, 0], f_extend_Gram_adjusted[0, 0]], "--", color="b", lw=1.6)
legend_elements = [
    Line2D([0], [0], color="k", lw=2.2, label="Original Function"),
    Line2D([0], [0], color="b", lw=2.2, label="FC-Gram Extension"),
    Line2D([0], [0], color="g", lw=2.2, label="FC-Legendre Extension"),
]
legend = plt.legend(handles=legend_elements, fontsize=19)
plt.xlim([-0.28, 1.31])
plt.ylim([-3.1, 2.6])
ax = plt.gca()
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.tick_params(axis="x", which="major", labelsize=19)
ax.tick_params(axis="y", which="major", labelsize=19)
plt.xticks([-0.25, 0, 1, 1.25], ["-0.25", "0", "1", "1.25"])
plt.yticks([-2, 2])
plt.tight_layout()
plt.show()
plot fourier continuation

Creating an example of 2D non-periodic function

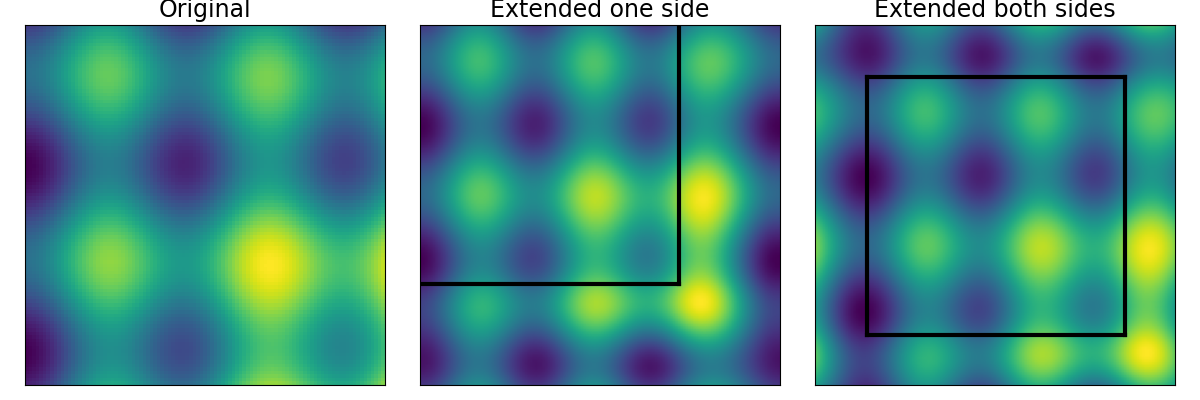
We consider f(x,y) = sin(12x) - cos(14y) + 3xy on the domain [0,1]×[0,1]. This function is not periodic on the unit square, making it suitable for testing 2D Fourier continuation methods.

length_signal = 101  # Length of the signal in each dimension
add_pts = 50  # Number of additional points for continuation in each dimension
batch_size = 3  # Batch size for processing multiple signals

# Create the 2D coordinate grids
x = torch.linspace(0, 1, length_signal).view(1, length_signal, 1).repeat(batch_size, 1, length_signal)
y = torch.linspace(0, 1, length_signal).view(1, 1, length_signal).repeat(batch_size, length_signal, 1)

# Define the 2D test function
f = torch.sin(12 * x) - torch.cos(14 * y) + 3 * x * y

Extending the signal

We use the FC-Legendre and FC-Gram Fourier continuation layers to extend the signal.

# FC-Legendre: Uses Legendre polynomial basis for 2D continuation
Extension_Legendre = FCLegendre(d=3, n_additional_pts=add_pts)
f_extend_Legendre = Extension_Legendre(f, dim=2)

# FC-Gram: Uses Gram polynomial basis for 2D continuation
Extension_Gram = FCGram(d=3, n_additional_pts=add_pts)
f_extend_Gram = Extension_Gram(f, dim=2)

Visualizing the 2D Fourier continuation results

We plot the original function and both continuation methods to compare their effectiveness in creating smooth 2D periodic extensions. Black lines delineate the original domain boundaries.

fig, axs = plt.subplots(figsize=(15, 5), nrows=1, ncols=3)

# Plot the original function
axs[0].imshow(f[0])
axs[0].set_title(r"Original Function", fontsize=15.5)
axs[1].imshow(f_extend_Legendre[0])
axs[1].plot([add_pts//2, length_signal + add_pts//2], [add_pts//2, add_pts//2], "-", color="k", lw=3)
axs[1].plot([add_pts//2, add_pts//2], [add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[1].plot([add_pts//2, length_signal + add_pts//2], [length_signal + add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[1].plot([length_signal + add_pts//2, length_signal + add_pts//2], [add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[1].set_title(r"FC-Legendre Extension", fontsize=15.5)
axs[2].imshow(f_extend_Gram[0])
axs[2].plot([add_pts//2, length_signal + add_pts//2], [add_pts//2, add_pts//2], "-", color="k", lw=3)
axs[2].plot([add_pts//2, add_pts//2], [add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[2].plot([add_pts//2, length_signal + add_pts//2], [length_signal + add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[2].plot([length_signal + add_pts//2, length_signal + add_pts//2], [add_pts//2, length_signal + add_pts//2], "-", color="k", lw=3)
axs[2].set_title(r"FC-Gram Extension", fontsize=15.5)
for ax in axs.flat:
    ax.set_xticks([])
    ax.set_yticks([])
plt.subplots_adjust(wspace=0.05)  # Reduce white space between plots
plt.show()
Original Function, FC-Legendre Extension, FC-Gram Extension

Creating an example of a 3D function

Here we consider f(x,y,z) = exp(-2z) + 2xz + sin(12xy) + y sin(10yz) which is not periodic on [0,1]x[0,1]x[0,1]

batch_size = 2
length_signal = 101
add_pts = 50

# Create 3D grid
x = torch.linspace(0, 1, length_signal).view(1, length_signal, 1, 1).repeat(batch_size, 1, length_signal, length_signal)
y = torch.linspace(0, 1, length_signal).view(1, 1, length_signal, 1).repeat(batch_size, length_signal, 1, length_signal)
z = torch.linspace(0, 1, length_signal).view(1, 1, 1, length_signal).repeat(batch_size, length_signal, length_signal, 1)

# Create 3D function
f = torch.exp(-2 * z) + 2 * z * x + torch.sin(12 * x * y) + y * torch.sin(10 * y * z)

Extending the signal

We use the FC-Legendre and FC-Gram Fourier continuation layers to extend the signal.

Extension_Legendre = FCLegendre(d=3, n_additional_pts=add_pts)
f_extend_Legendre = Extension_Legendre(f, dim=3)

Extension_Gram = FCGram(d=3, n_additional_pts=add_pts)
f_extend_Gram = Extension_Gram(f, dim=3)

Plot the FC-Legendre and FC-Gram results for 3D

We also add white lines to deliminate the original signal

f_min = f.min().item()
f_max = f.max().item()
f_ext_legendre_min = f_extend_Legendre.min().item()
f_ext_legendre_max = f_extend_Legendre.max().item()
f_ext_gram_min = f_extend_Gram.min().item()
f_ext_gram_max = f_extend_Gram.max().item()
global_min = min(f_min, f_ext_legendre_min, f_ext_gram_min)
global_max = max(f_max, f_ext_legendre_max, f_ext_gram_max)

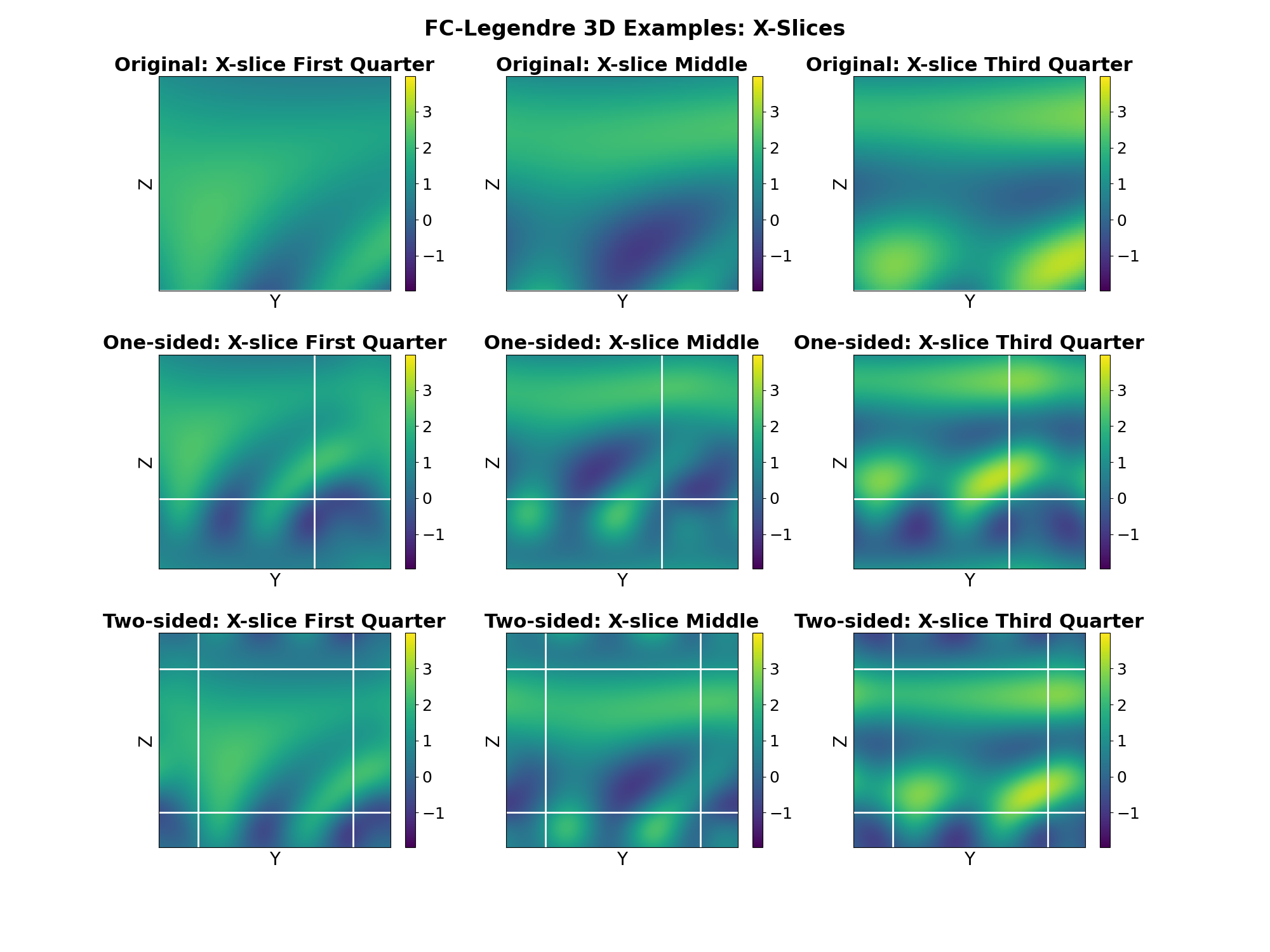
Figure for X slices

fig = plt.figure(figsize=(24, 20))
slice_indices = [length_signal//4, length_signal//2, 3*length_signal//4]
slice_names = ["First Quarter", "Middle", "Third Quarter"]

for i, (idx, name) in enumerate(zip(slice_indices, slice_names)):
    # Original function - X-slice
    ax = fig.add_subplot(3, 3, i + 1)
    im = ax.imshow(f[0, idx, :, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"Original: X-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("Y", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Legendre extension - X-slice
    ax = fig.add_subplot(3, 3, i + 4)
    ext_idx = idx + add_pts//2
    im = ax.imshow(f_extend_Legendre[0, ext_idx, :, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Legendre: X-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("Y", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Gram extension - X-slice
    ax = fig.add_subplot(3, 3, i + 7)
    im = ax.imshow(f_extend_Gram[0, ext_idx, :, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Gram: X-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("Y", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

plt.subplots_adjust(hspace=0.15, wspace=0.05, top=0.95)
plt.show()
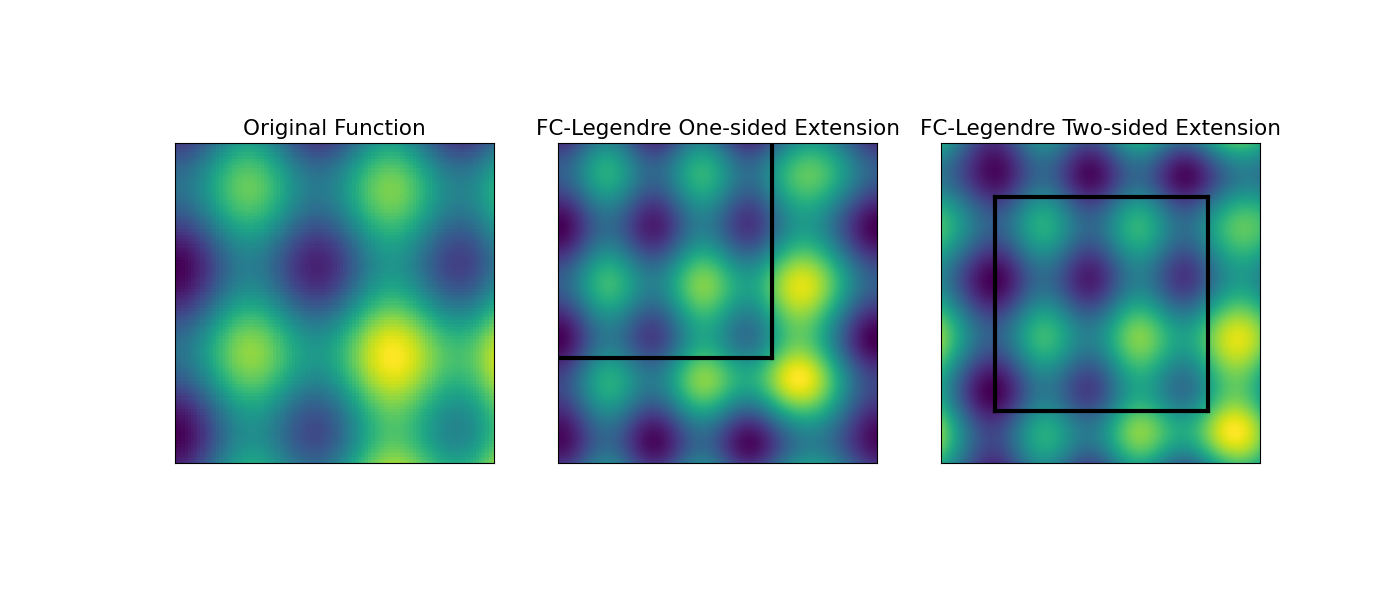
Original: X-slice First Quarter, FC-Legendre: X-slice First Quarter, FC-Gram: X-slice First Quarter, Original: X-slice Middle, FC-Legendre: X-slice Middle, FC-Gram: X-slice Middle, Original: X-slice Third Quarter, FC-Legendre: X-slice Third Quarter, FC-Gram: X-slice Third Quarter

Figure for Y-slices

fig2 = plt.figure(figsize=(24, 20))

for i, (idx, name) in enumerate(zip(slice_indices, slice_names)):
    # Original function - Y-slice
    ax = fig2.add_subplot(3, 3, i + 1)
    im = ax.imshow(f[0, :, idx, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"Original: Y-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Legendre extension - Y-slice
    ax = fig2.add_subplot(3, 3, i + 4)
    ext_idx = idx + add_pts//2
    im = ax.imshow(f_extend_Legendre[0, :, ext_idx, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Legendre: Y-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Gram extension - Y-slice
    ax = fig2.add_subplot(3, 3, i + 7)
    im = ax.imshow(f_extend_Gram[0, :, ext_idx, :].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Gram: Y-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Z", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

plt.subplots_adjust(hspace=0.15, wspace=0.05, top=0.95)
plt.show()
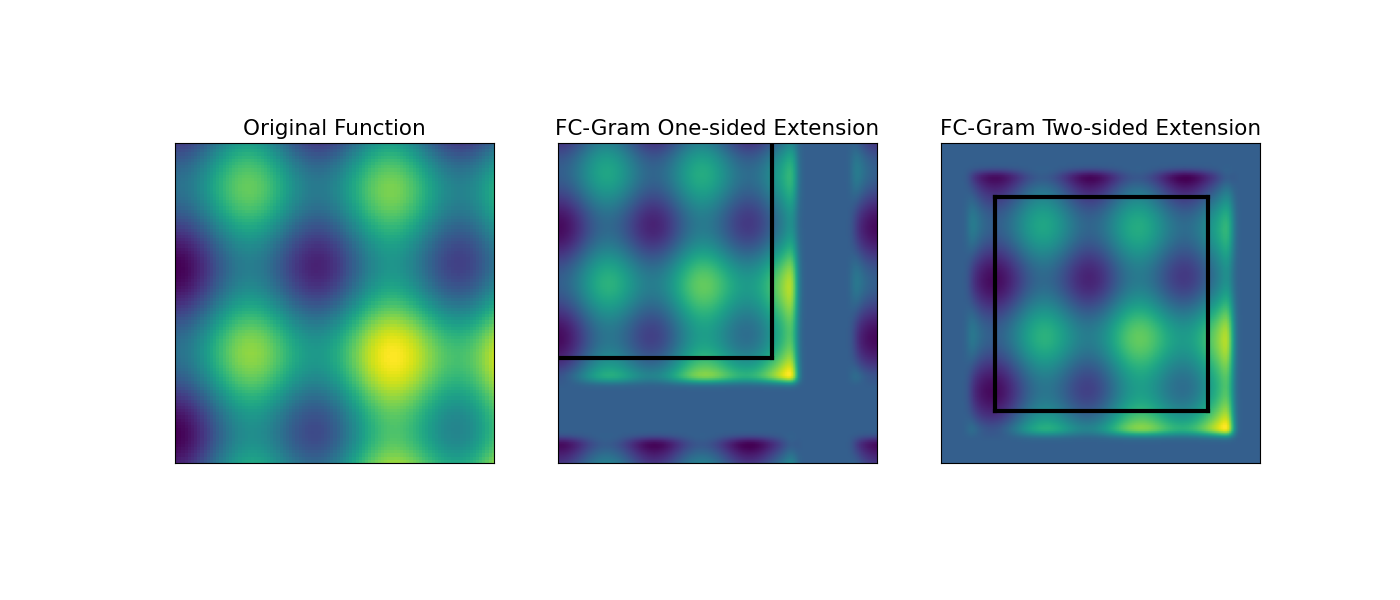
Original: Y-slice First Quarter, FC-Legendre: Y-slice First Quarter, FC-Gram: Y-slice First Quarter, Original: Y-slice Middle, FC-Legendre: Y-slice Middle, FC-Gram: Y-slice Middle, Original: Y-slice Third Quarter, FC-Legendre: Y-slice Third Quarter, FC-Gram: Y-slice Third Quarter

Figure for Z-slices

fig3 = plt.figure(figsize=(24, 20))

for i, (idx, name) in enumerate(zip(slice_indices, slice_names)):
    # Original function - Z-slice
    ax = fig3.add_subplot(3, 3, i + 1)
    im = ax.imshow(f[0, :, :, idx].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"Original: Z-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Y", fontsize=20)
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Legendre extension - Z-slice
    ax = fig3.add_subplot(3, 3, i + 4)
    ext_idx = idx + add_pts//2
    im = ax.imshow(f_extend_Legendre[0, :, :, ext_idx].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Legendre: Z-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Y", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

    # FC-Gram extension - Z-slice
    ax = fig3.add_subplot(3, 3, i + 7)
    im = ax.imshow(f_extend_Gram[0, :, :, ext_idx].numpy(), cmap="viridis", aspect="auto", vmin=global_min, vmax=global_max)
    ax.set_title(f"FC-Gram: Z-slice {name}", fontsize=22, fontweight="bold")
    ax.set_xlabel("X", fontsize=20)
    ax.set_ylabel("Y", fontsize=20)
    # Draw boundary lines
    ax.axhline(y=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axhline(y=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.axvline(x=length_signal + add_pts//2, color="white", linewidth=2, linestyle="-")
    ax.set_xticks([])
    ax.set_yticks([])
    cbar = plt.colorbar(im, ax=ax)
    cbar.ax.tick_params(labelsize=18)

plt.subplots_adjust(hspace=0.15, wspace=0.05, top=0.95)
plt.show()
Original: Z-slice First Quarter, FC-Legendre: Z-slice First Quarter, FC-Gram: Z-slice First Quarter, Original: Z-slice Middle, FC-Legendre: Z-slice Middle, FC-Gram: Z-slice Middle, Original: Z-slice Third Quarter, FC-Legendre: Z-slice Third Quarter, FC-Gram: Z-slice Third Quarter

Total running time of the script: (0 minutes 2.105 seconds)

Gallery generated by Sphinx-Gallery